Theorem Hunt
SoME, Linear Algebra ·Introduction
Hi, I live in the world of Linear Algebra. I take on many shapes and sizes. Most notably a square. Perhaps I sound familiar. What am I? Do I hear matrix? That is right! Call me A.
I recently met with L, a linear transformation, and spoke with him about a treasure that only a select few had seen before. L and I wanted to see it too. We managed to get a hold of the scroll that leads to the treasure, shown in Figure 1. I have seen some of the imagery in this document before, so not all of it is unfamiliar.
This treasure is a theorem of great mathematical importance as other results in the mathematical universe, but does not seem to get as much attention as it should. It has been said that it does not deserve the name bestowed to it. Yet, this theorem is connected to finding the solutions to a linear system of equations.
L and I decided to meet and seek the treasure with two things in mind:
- explain the building blocks of the theorem
- illustrate the theorem to get a better understanding
L reminded me of his vector mapping rule, shown in Figure 2, and questioned me with the following prompt:
Exercise 1. There are many kinds of vectors in the mathematical world. Describe at least three.
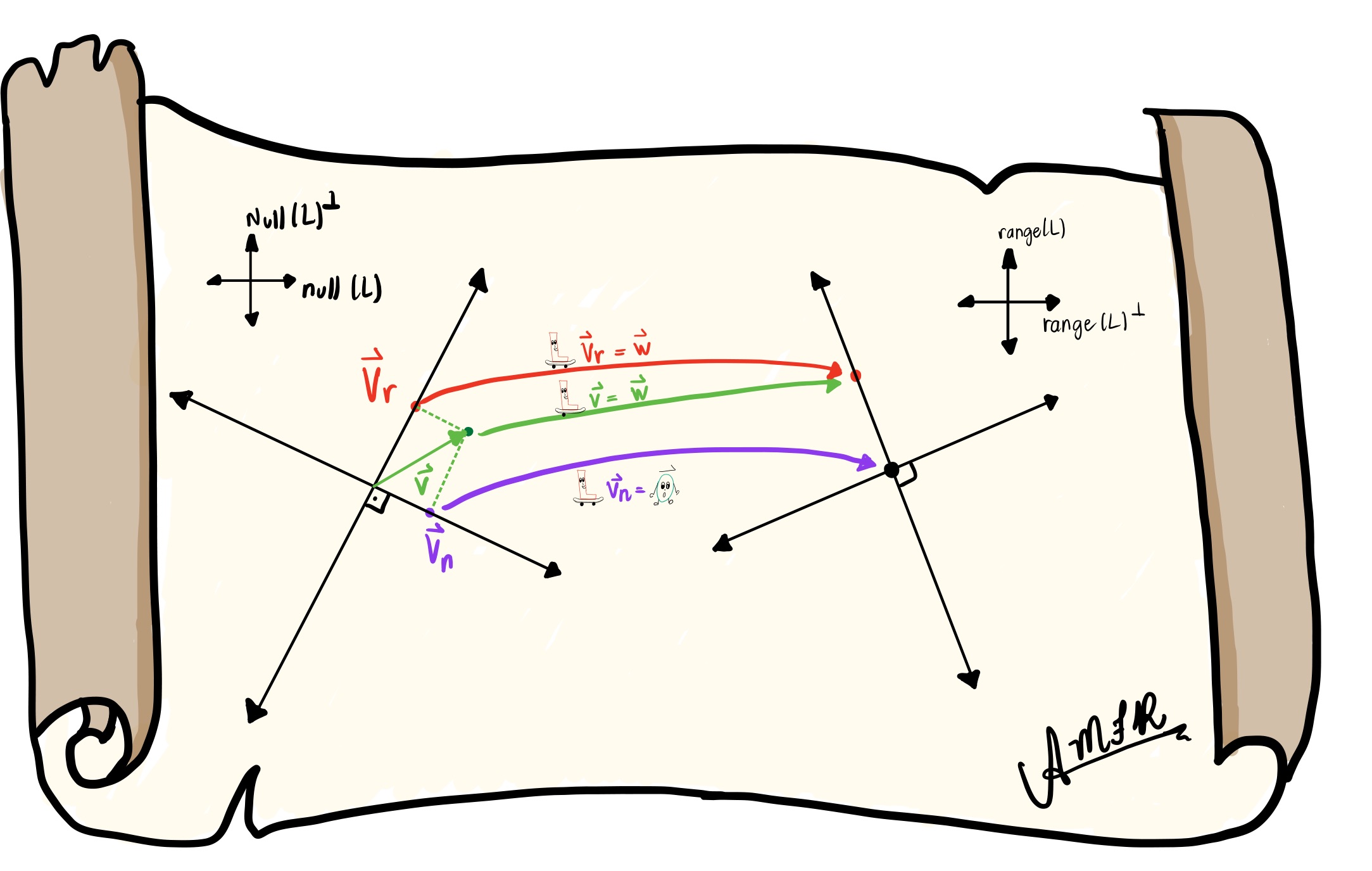
Figure 1. A depiction of vector spaces.
Maps and Vector Spaces
In our world, there are many linear transformations that travel to a lot of different places, accompanying vectors and connecting their vector spaces to one another. The vector spaces are like machines with advanced communication protocols. As vectors are paired between vector spaces, energy is shared such that it enables effective communication. It is said that if all vectors are paired in an efficient format, then the linear transformation is known as a bijection.
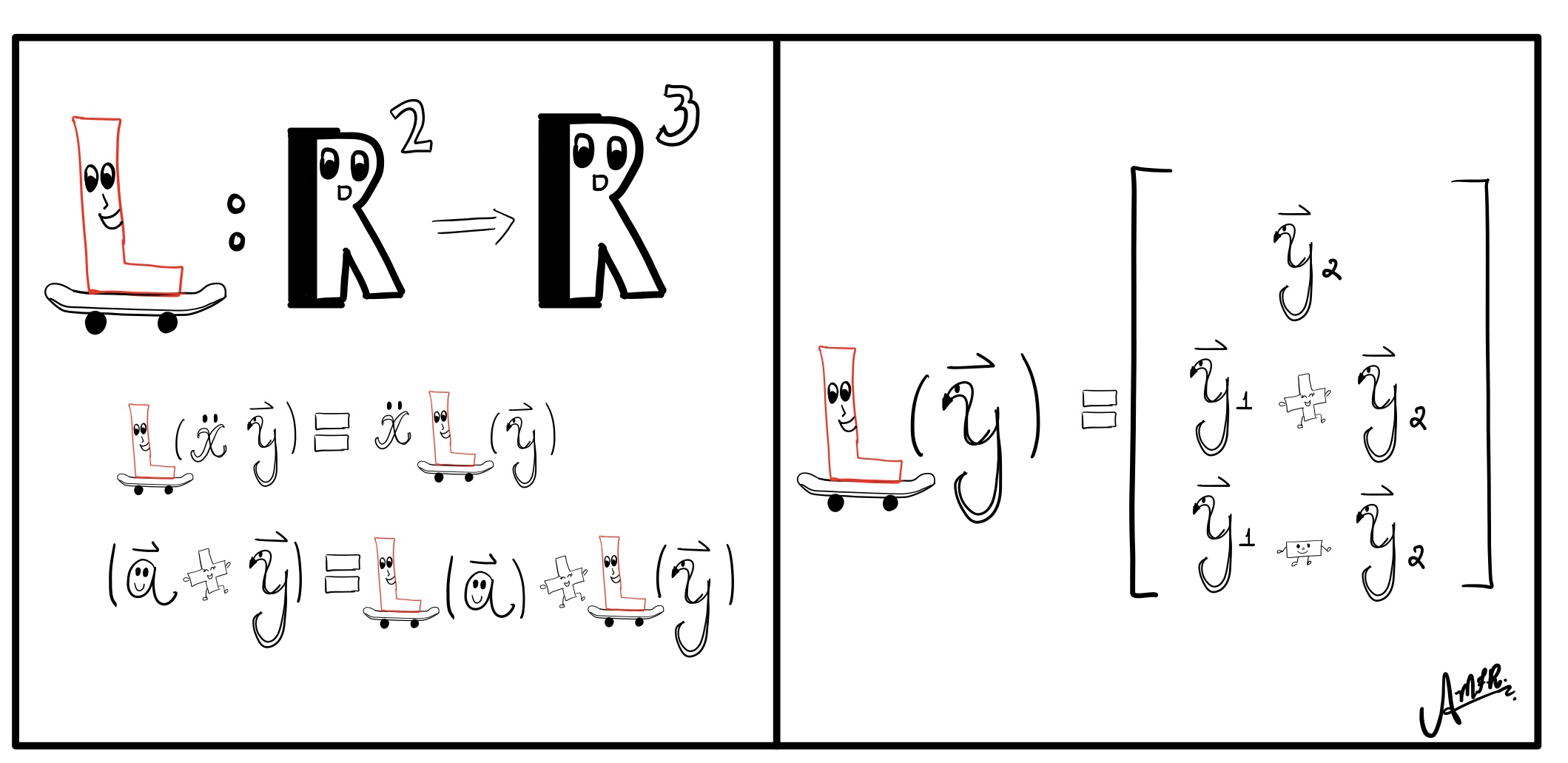
Figure 2. L’s vector mapping rule from \(V\) to \(W\).
On the day L and I set out to travel, I learned of two vector spaces, \(V\) and \(W\). \(V\) was located atop of mountains whereas \(W\) was somewhere else near a body of water. To get to the mountains, we proceeded to a station of pods, oval-shaped vehicles. Once there, I located a vacant one, but it seemed to be out of commission. I tried asking for help from a nearby operator, but it stood in place, redirecting the flow of pods leaving and entering the area.
The pod was indeed in working conditions, as it required an answer to the following prompt:
Exercise 2. Confirm the properties of linear transformations.
Shining Subspaces
L answered the prompt and we were good to go to the mountains. After our flight, we stepped onto the snowy terrain and the pod automatically returned to the pod station.

We entered a cottage where we met the zero vector of \(V\), \(\mathbf{0}_{V}\). He told us that \(V\) had lost communication with \(W\) and its zero vector, \(\mathbf{0}_{W}\). I assured him that we would do our best to establish a connection. L would take care of performing the necessary calculations. As I turned to L, the scroll fell out of the bag I brought with me. \(\mathbf{0}_{V}\) picked up the scroll and immediately recognized it. Unfortunately, \(\mathbf{0}_{V}\) did not know much about it.
L began to take individual vectors from the input space and transformed them to vectors in the output space. After a while, \(\mathbf{0}_{V}\) wanted to see our progress. We showed him an image of vectors that had been paired with their friend, shown in Figure 3:
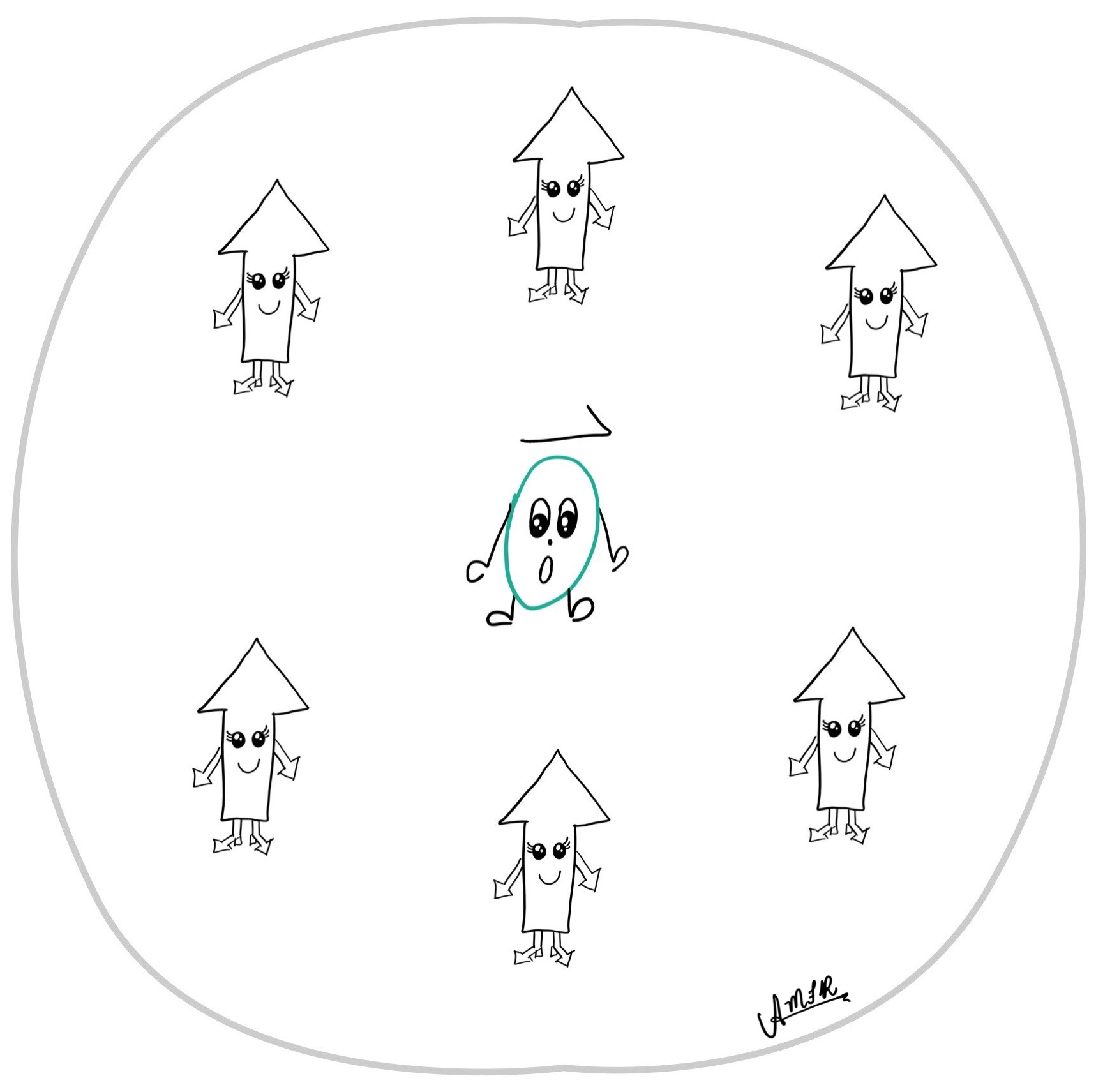
Figure 3. Vectors in \(W\).
\(\mathbf{0}_{V}\) was pleased by our work. He made a note that perhaps a boundary surrounding the grouped vectors was significant. I agreed and informed him that this collection of vectors was known as the range or image (of L). We saw that the scroll showed a red arrow pointing to this “north-to-south” direction on the right hand side axis. While we did not fully agree on the name, we did agree that more vectors needed to be transformed to get a clearer picture.

L noticed that a lot of vectors could map to \(\mathbf{0}_{W}\) and called them similar. I confirmed that the vectors that looked similar are scalar multiples of one another. With a glance over to the scroll, L pointed to the purple arrow going from the “west-to-east” direction on the left hand side over to the intersection of lines on the right hand side. This confirmed another part of the scroll: the collection of vectors that mapped to \(\mathbf{0}_{W}\) is called the nullspace of L. (Fun fact: null is synonymous with zero, nothing, nada, empty, or nil.) Moreover, I noted that the range and nullspace of L are special: they are subspaces.
We discussed the concept of a vector (sub)space’s size, known as dimension. For example, for \(\mathbb{R}^{3}\), its dimension is \(3\). For \(P_{n}(\mathbb{R})\), its dimension is \(n + 1\), where \(n\) is a natural number.
Now, L noticed something about the vectors that mapped to \(\mathbf{0}_{W}\). \(\mathbf{0}_{V}\) and I listened as L reported that the dimension of the collection of these vectors was smaller than the vector space \(V\). He also noticed that the image had the potential to be smaller than or equal to the dimension of \(W\). These were two excellent observations.
Furthermore, there is an important relationship between the dimensions of \(V\), the range of L, and the nullspace of L, given by,
\[\text{dim}\ \text{range}(L) + \text{dim}\ \text{null}(L) = \text{dim}\ V \text{.}\]This is known as the dimension sum theorem.
\(\mathbf{0}_{V}\) and L were happy after my explanation. In all of this excitement, we were startled by an incoming transmission from \(W\). A vector \(\mathbf{w}\) looked angry. She told us that she was concerned that she might not be paired with a friend through L’s transformation. She also mentioned someone that might be helpful in deciphering our beige-colored document. L and I looked at one another and wondered if she was on to something. After a bit of questioning, we set course for a lighthouse, the home of where an \(\text{L}^{\ast}\) (L star) lived. L and I were determined to find out if \(\mathbf{w}\) gets a friend.
With another nearby pod station, we took a pod to the lighthouse, not before answering the following prompt:
Exercise 3. The vector that generates the scalar multiples is called the basis vector. Determine if the basis vector for the nullspace of L exists as a two element list and state its dimension.
Adjoint Boulevard
Up to this point, we have addressed most of the scroll’s mysteriousness. We have been looking in the directions of both the nullspace and range, as depicted by the larger axes on the scroll. What about the other directions? In particular, the “north-to-south” direction on the left axis and the “west-to-east” direction on the right axis. In addition, the upside-down “t” symbol, \(\perp\), on the smaller axes is unclear. We cannot forget about the green arrow as well.
Landing outside the lighthouse, it began raining. We entered and made our way to the top. L and I saw someone staring into the ocean. It was \(\text{L}^{\ast}\). I showed \(\text{L}^{\ast}\) the scroll and briefed her about the things we had understood thus far. “Those are some good observations.” she said.
She told us that she visits the vector space \(W\) often and that \(\mathbf{w}\) is an old friend. \(\text{L}^{\ast}\) sung, “Let \(V\) and \(W\) be (finite-dimensional) vector spaces equipped with an inner product\(\dots\)” It turned out that many vectors like to know the distance between one another with the help of an inner product. Vectors can also know if they are orthogonal or perpendicular to each other.
\(\text{L}^{\ast}\) continued, comparing L and herself. She claimed that L transformed vectors from \(V\) to \(W\), whereas she transformed vectors from \(W\) to \(V\). In other words,
\[L\colon V \to W \quad\text{and}\quad L^{\ast}\colon W \to V \text{.}\]\(\text{L}^{\ast}\) was not necessarily an inverse transformation. \(\text{L}^{\ast}\) is an adjoint. Because of this connection between \(V\) and \(W\), \(\text{L}^{\ast}\) showed that she had her own nullspace and range. These were the “unknown” directions referenced earlier. \(\text{L}^{\ast}\) called them orthogonal complements. I realized that she was referring to the upside-down “t” symbol in the scroll.
\(\text{L}^{\ast}\) remarks on \(\mathbf{w}\)’s concerns. The problem we wanted to solve can be represented mathematically as the equation \(L \mathbf{v} = \mathbf{w}\). \(\text{L}^{\ast}\) pointed to the green arrow in the scroll and noted that the addition of the vector in the nullspace of L, \(\mathbf{v}_{n}\), and the vector in the range of \(\text{L}^{\ast}\), \(\mathbf{v}_{r}\), provided a general solution to \(L \mathbf{v} = \mathbf{w}\). In other words, solving \(L \mathbf{v} = \mathbf{w}\) is the same as solving \(L \left(\mathbf{v}_{r} + \mathbf{v}_{n}\right) = \mathbf{w}\).
\(\text{L}^{\ast}\) decided to brew some tea and gave us the following prompt:
Exercise 4. Present the simplest inner product for vectors in Euclidean Space.
The Fundamental Theorem of Linear Algebra
L and I got to thinking about everything \(\text{L}^{\ast}\) had communicated. Ultimately, the key to the treasure involves the nullspaces of L and \(\text{L}^{\ast}\). Now knowing that \(\mathbf{w}\) lived in the orthogonal complement to the nullspace of \(\text{L}^{\ast}\), to determine if she was going to be paired with a friend, we needed to find out if she was orthogonal to all vectors in the nullspace of \(\text{L}^{\ast}\). Finally, the treasure had been found. It was not something tangible, but rather a powerful idea.
\(\text{L}^{\ast}\) summoned her pod and took \(L\) and I back to the mountains, where all of the information was reiterated to \(\mathbf{w}\), \(\mathbf{0}_{V}\), and \(\mathbf{0}_{W}\), who had made an appearance upon our arrival. I thanked \(\text{L}^{\ast}\) for her help and asked her what prompt she answered in order to activate her pod.
She smiled and said,
Exercise 5. Vector Spaces are amazing. Name vector spaces that are infinite dimensional.
Thanks for reading! This story was written by Aline Rohloff and Gustavo Sopena for the Summer of Math Exposition 2022 (SoME2). If you have any questions about the story, send an email to Gustavo Sopena at gsopena7@gmail.com. Banner, figures, and character images by Aline Rohloff.