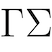Peg Solitaire

Abstract Algebra, Python · 01 Aug 2019

Summary:

Project is an implementation of peg solitaire in Python
Program is designed to replace playing games by hand
Program helps our team research the game and its winnability

As per the README:

This project is an implementation of peg solitaire in python with some modifications. In this project, pegs are colored arbitrarily from a finite set of colors labeled as integer values. The objective is to have one peg remaining irrespective of the color of the peg after a series of moves. That is, pegs can jump over other pegs into an empty vertex on a graph provided that the vertices they occupy are connected to one another. Depending on the color of the pegs involved, pegs can either change into another peg of a different color or are removed.

The program was developed so that it would help our student research team at CSU Fullerton determine when a playthrough of peg solitaire resulted in a win. We started playing the game by hand, but as we introduced mathematical graphs, the games increase in complexity.

The main feature of the program is playing games. The program does this by looking at the peg positions on the board (graph) and builds a list of all possible moves in which pegs can move. Once it executes said moves, a list of new peg positions is built and the program repeats this process until no new peg positions can be made. If a sequence of moves can be found that leaves one peg on the board, then the game is considered winnable.

Another change incorporated by this program is the ability to have pegs be distinct colors. Different colors translates into different ways to remove pegs from the board. One way the pegs are removed from the board is discussed in our paper “Peg Solitaire in Three Colors on Graphs” where we use modular arithmetic. This color mechanism continues to be researched by our team and other students.

I started working on this project in Summer 2019 and since then, I work on the program on my spare time, adding features I think would be beneficial to our work. Our team continue to research other modifications to peg solitaire in addition to the color mechanic and do not see signs of slowing down development.